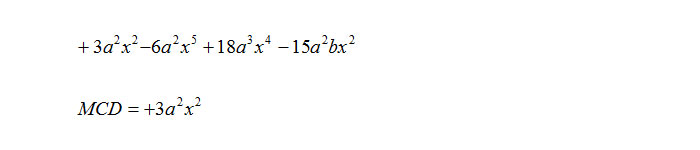Raccoglimento a fattor comune

Il raccoglimento a fattor comune è un'operazione matematica che consente di mettere in evidenza una parte letterale e/o una parte numerica che moltiplica tutto ciò che la segue, e si basa sulla proprietà distributiva della moltiplicazione rispetto all'addizione. Si divide in raccoglimento totale e raccoglimento parziale.

Il raccoglimento totale è la più semplice operazione di scomposizione di un polinomio in fattori, che consiste nell'individuare, se esiste, il monomio massimo comun divisore; per esempio: ${\displaystyle AB AC=A(B C).}$

Il raccoglimento parziale si ha quando non tutti i termini di un polinomio hanno dei fattori comuni, ma solo alcuni di essi; si procede quindi prima con un raccoglimento parziale raggruppando le parti in comune. La procedura è finalizzata nell'evidenziare, dopo questo primo passaggio, una parte che in un secondo tempo può essere raccolta totalmente. Per esempio, si consideri il seguente polinomio: ${\displaystyle ax bx ay by.}$

I primi due termini hanno in comune un termine ${\displaystyle x}$, il terzo e il quarto un termine ${\displaystyle y}$; procedendo col raccoglimento, si ottiene:

${\displaystyle x(a b) y(a b)=(x y)(a b).}$

Nell'ultimo passaggio, dato che sia la ${\displaystyle x}$ che la ${\displaystyle y}$ sono moltiplicate per il fattore ${\displaystyle a b}$, si può raccogliere quest'ultimo e si ottiene il prodotto ${\displaystyle (x y)(a b)}$.

Utilità

L'operazione di raccoglimento a fattor comune è particolarmente utile perché consente di semplificare anche di molto dei polinomi che, se non ridotti a una forma più accessibile, risulterebbero molto difficili da trattare.

• Si consideri come esempio il binomio:

${\displaystyle 2x^{3} 10x^{2}.}$

Qualora si volesse trovarne gli zeri (o discuterne il segno), è possibile raccogliere a fattor comune il massimo comun divisore tra i monomi che compongono il binomio; a esempio:

${\displaystyle 2x^{3} 10x^{2}=0\,\,\to \,\,2x^{2}(x 5)=0.}$

Per la legge di annullamento del prodotto, l'equazione è soddisfatta per ${\displaystyle x=0\,\,\lor \,\,x=-5}$.

• Analogamente è possibile fare uso del raccoglimento a fattor comune per semplificare le frazioni:

riprendendo in parte l'esempio precedente e considerando la frazione:

${\displaystyle {\frac {2x^{3} 10x^{2}}{x^{3} 5x^{2} x 5}},}$

si può procedere col raccoglimento totale a numeratore (visto prima) e con un raccoglimento prima parziale e poi totale a denominatore:

${\displaystyle {\frac {2x^{2}(x 5)}{x^{2}(x 5) x 5}}={\frac {2x^{2}(x 5)}{(x 5)(x^{2} 1)}}.}$

È ora possibile semplificare sia a numeratore che a denominatore il fattore ${\displaystyle (x 5)}$, a patto però di calcolare prima il campo di esistenza, ponendo ${\displaystyle x 5\neq 0\,\,\implies \,\,x\neq -5}$:

${\displaystyle {\frac {2x^{2}(x 5)}{(x 5)(x^{2} 1)}}={\frac {2x^{2}}{x^{2} 1}}.}$

Note

Bibliografia

• Massimo Bergamini, Graziella Barozzi, Anna Trifone, Matematica.blu (seconda edizione) Vol.1, Zanichelli - Bologna, 2018, ISBN 978-88-08-22085-1.
• Marzia Re Fraschini, Gabriella Grazzi, I principi della matematica (Volume 3), Atlas, 2012, ISBN 978-88-268-1711-8.

Voci correlate

• Regola di Ruffini
• Polinomi
• Equazione